J'ai choisi celui la pour le challenge de juin
 モモンガ / Frying Squirrel -CP- by Arisawa Yuga, sur Flickr
モモンガ / Frying Squirrel -CP- by Arisawa Yuga, sur Flickr モモンガ / Frying Squirrel by Arisawa Yuga, sur Flickr
モモンガ / Frying Squirrel by Arisawa Yuga, sur Flickr モモンガ / Frying Squirrel by Arisawa Yuga, sur Flickr
モモンガ / Frying Squirrel by Arisawa Yuga, sur FlickrBon plis
 モモンガ / Frying Squirrel -CP- by Arisawa Yuga, sur Flickr
モモンガ / Frying Squirrel -CP- by Arisawa Yuga, sur Flickr モモンガ / Frying Squirrel by Arisawa Yuga, sur Flickr
モモンガ / Frying Squirrel by Arisawa Yuga, sur Flickr モモンガ / Frying Squirrel by Arisawa Yuga, sur Flickr
モモンガ / Frying Squirrel by Arisawa Yuga, sur FlickrNon, c'est plus facile avec mon Origami Drawtudor a écrit :Et une autre question: est-ce un gros handicap de ne pas utiliser Oripa pour déchiffrer ce genre de CP?
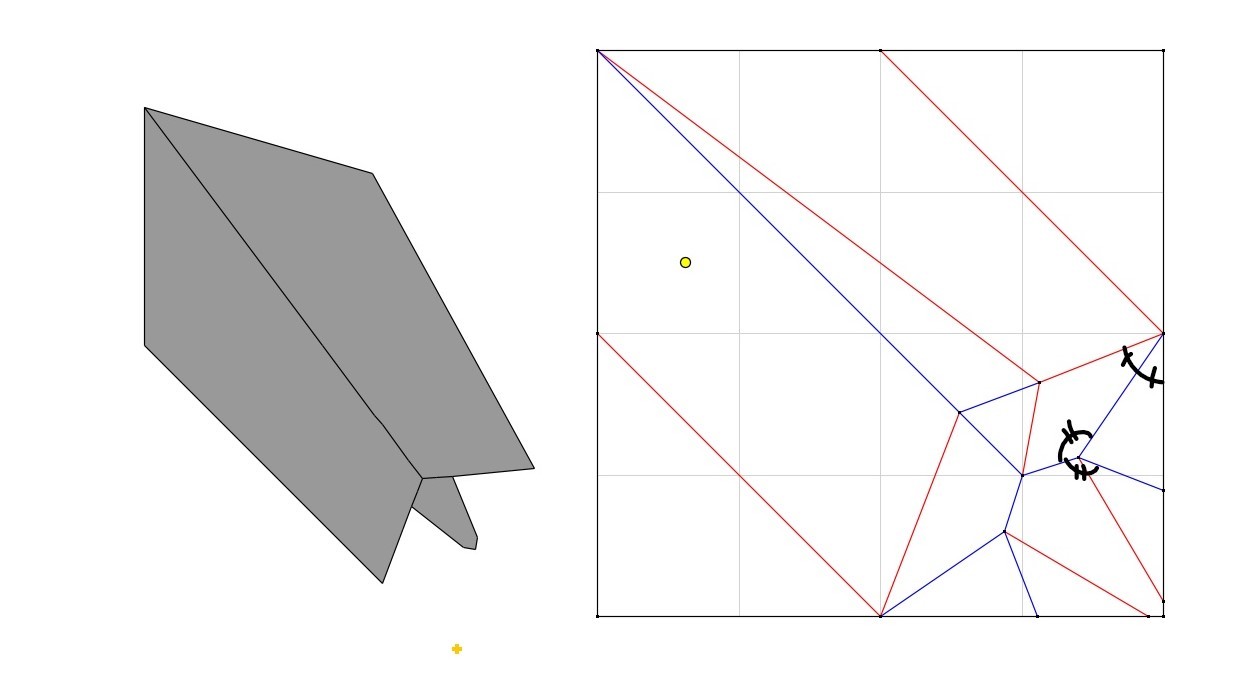
je dirait qu'oripa (ou autres logiciel de pliage) facilitent beaucoup le travail de vérification alors pourquoi s'en privertudor a écrit :est-ce un gros handicap de ne pas utiliser Oripa pour déchiffrer ce genre de CP?
Désolé, je t'ai envoyé sur une fausse piste avec cette image tirée du blog. Ce sont deux autres angles égaux qu'il faut voir, FGJ et FGE, ce qui veut dire que GJ et GE sont symétriques par rapport à CF. C'est là qu'intervient l'axiome 5. Je sais qu'on n'est pas très habitué à cette construction mais tout est déjà là sur le schéma que tu as annoté. Il suffit d'imaginer qu'on plie suivant CF et on voit où va quoi.tudor a écrit :J'ai bien vu les angles égaux sur le schéma du blog, mais je n'arrive pas encore à en tirer la position de G...
Ça aurait pu... mais ce n'est pas le cas ! Ça donnerait de nouveau une tête trop aplatie avec un menton trop large : La tête est en fait construite sur une base de poisson, donc en 22.5. Mais ces deux angles sont très proches et on ne peut voir la différence qu'en mesurant précisément. D'où l'importance ici d'un diagramme exact, dessiné avec un logiciel qui construit correctement les angles.rouchka a écrit :Maintenant je pense que HA est symétrique a CF par rapport a la 2e diagonale
Aha! J'ai pigé. En tout cas, je le pense.rouchka a écrit :Il s'agit donc de faire pivoter CE autour de C jusqu'à ce que E soit sur GJ. Et là on obtient le pli CG. Bien vu Akira!

... Rouchka, ne pense pas que j'ignore tes conseils! C'est juste que je ne vois pas du toutrouchka a écrit :La référence de P se trouve alors sur le corp.